[试卷]第26章 反比例函数 章末综合练 2024-尊龙凯时人生就博

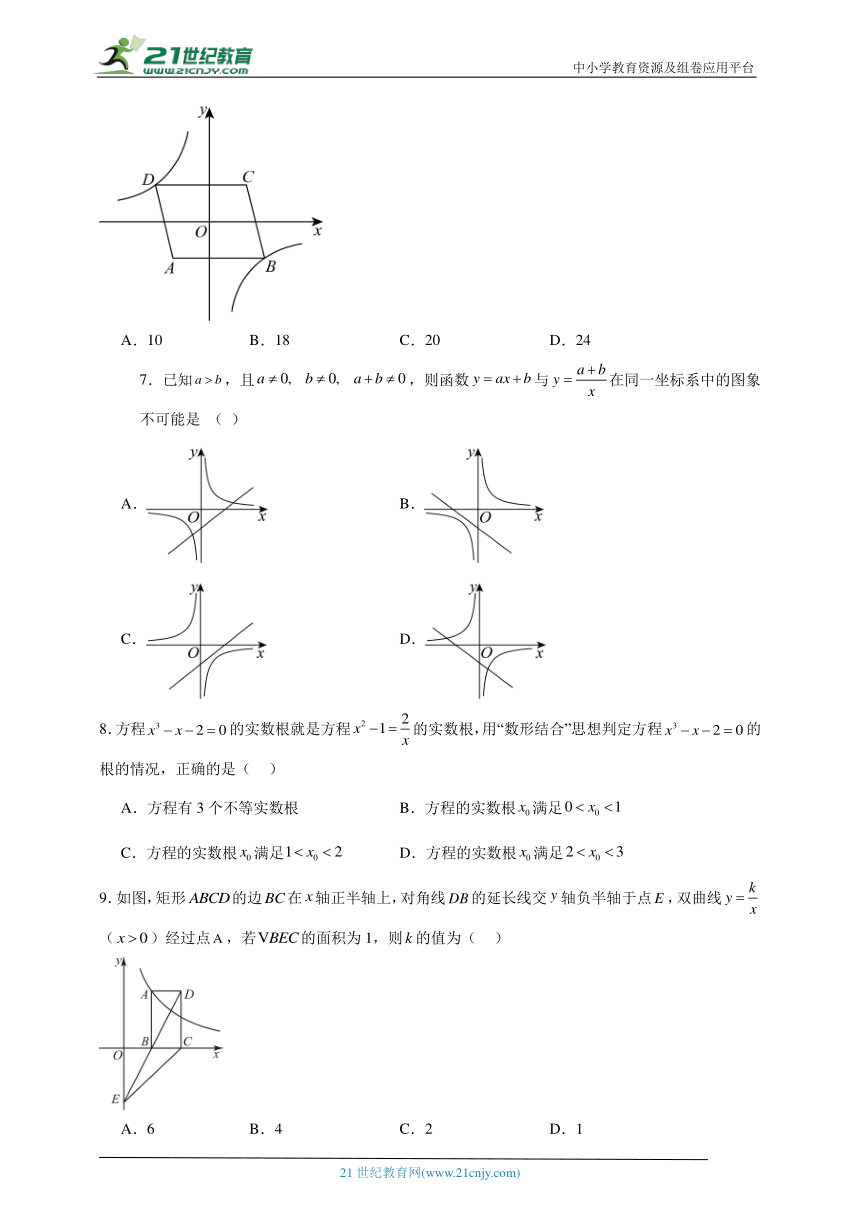
中小学教育资源及组卷应用平台 反比例函数 章末综合练 2024--2025 学年初中数学人教版九年级下册 一、单选题 1．下列关系中，是反比例函数的是（ ） a． b． c． d． 2．下列四个点中，在反比例函数y＝的图象上的是（　　） a．（﹣3，﹣2） b．（3，2） c．（﹣2，3） d．（﹣2，﹣3） 3．反比例函数经过点（2，1），则下列说法错误的是（　　） a．点（﹣1，﹣2）在函数图象上 b．函数图象分布在第一、三象限 c．y随x的增大而减小 d．当y≥4时，0＜x≤ 4．如图所示，四边形abcd的顶点都在坐标轴上，若ad∥bc，acd与bcd的面积分别为20和40，若双曲线y＝（k＜0，x＜0）恰好经过边ab的四等分点e（be＜ae），则k的值为（ ） a．﹣5 b．﹣10 c．﹣15 d．﹣20 5．已知反比例函数，如果在这个函数图象所在的每一个象限内，y的值都随x的增大而增大，那么k的取值可能是（　　） a．0 b．2 c．3 d．4 6．如图，在平面直角坐标系中，o为□abcd的对称中心，点a的坐标为(－2，－2)，ab=5，ab//x轴，反比例函数y=的图象经过点d，将□abcd沿y轴向下平移，使点c的对应点c′落在反比例函数的图象上，则平移过程中线段ac扫过的面积为(　　) a．10 b．18 c．20 d．24 7．已知，且，则函数与在同一坐标系中的图象不可能是 （ ） a． b． c． d． 8．方程的实数根就是方程的实数根，用“数形结合”思想判定方程的根的情况，正确的是（ ） a．方程有3个不等实数根 b．方程的实数根满足 c．方程的实数根满足 d．方程的实数根满足 9．如图，矩形的边在轴正半轴上，对角线的延长线交轴负半轴于点，双曲线（）经过点，若的面积为1，则的值为（ ） a．6 b．4 c．2 d．1 10．如图，正方形的顶点p，q分别在反比例函数和的图象上，点m，n在x轴上，交y轴于点g，连接交y轴于点h，若，则（ ） a． b． c． d．2 二、填空题 11．已知反比例函数 y=的图像都过a（1，3）则m= . 12．若点在函数图象上，那么的值为 ． 13．如图，已知反比例函数和，点是上任意一点，连接交于点，分别过点、作轴、轴的平行线，得到矩形，则矩形的面积是 ． 14．如图，a是反比例函数图象上的一点，ab垂直于x轴，垂足为b，ac垂直于y轴，垂足为c，若矩形aboc的面积为5，则k的值为 ． 15．如图，在平面直角坐标系中，函数y=（k＞0）的图象经过点a（1，2）、b两点，过点a作x轴的垂线，垂足为c，连接ab、bc．若三角形abc的面积为3，则点b的坐标为 ． 三、解答题 16．已知与成正比例，与成反比例，当时，；当时，． (1)求y与x的函数关系式； (2)当时，求y的值． 17．已知一艘轮船上装有120吨货物，轮船到达目的地后开始卸货．设平均卸货速度为（单位：吨/小时），卸完这批货物所需的时间为（单位：小时）． (1)求关于的函数表达式； (2)若要求不超过6小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？ (3)按6小时卸完船上的这批货物，卸货2小时后，根据实际情况，要求剩下的货物要在2小时内卸完，在剩下的时间内每小时要多卸多少吨货物？ 18．如图，一次函数 与反比例函数 的图象相交于，两点，连接，，延长交反比例函数图象于点c． (1)求一次函数的表达式与反比例函数的表达式； (2)当时，直接写出自变量x的取值范围为_____； (3)点p是x轴上一点，当时，请求出点p的坐标． 19．如图，菱形abcd的顶点a、b分别在y轴与x轴正半轴上，c、d在第一象限，轴，反比例函数的图象经过顶点d． (1)若， ①求反比例函数的解析式； ②证明：点c落在反比例函数的图象上； (2)若，，求菱形abcd的边长． 20．已知: 反比例函数经过点b(1,1) ． （1）求该反比例函数解析式； （2）连接ob，再把点a(2,0)与点b连接,将△oab绕点o按顺时针方向旋转135°得到△o，写出的中点p的坐标，试判断点p是否在此双曲 ... ...