[试卷]2024-尊龙凯时人生就博

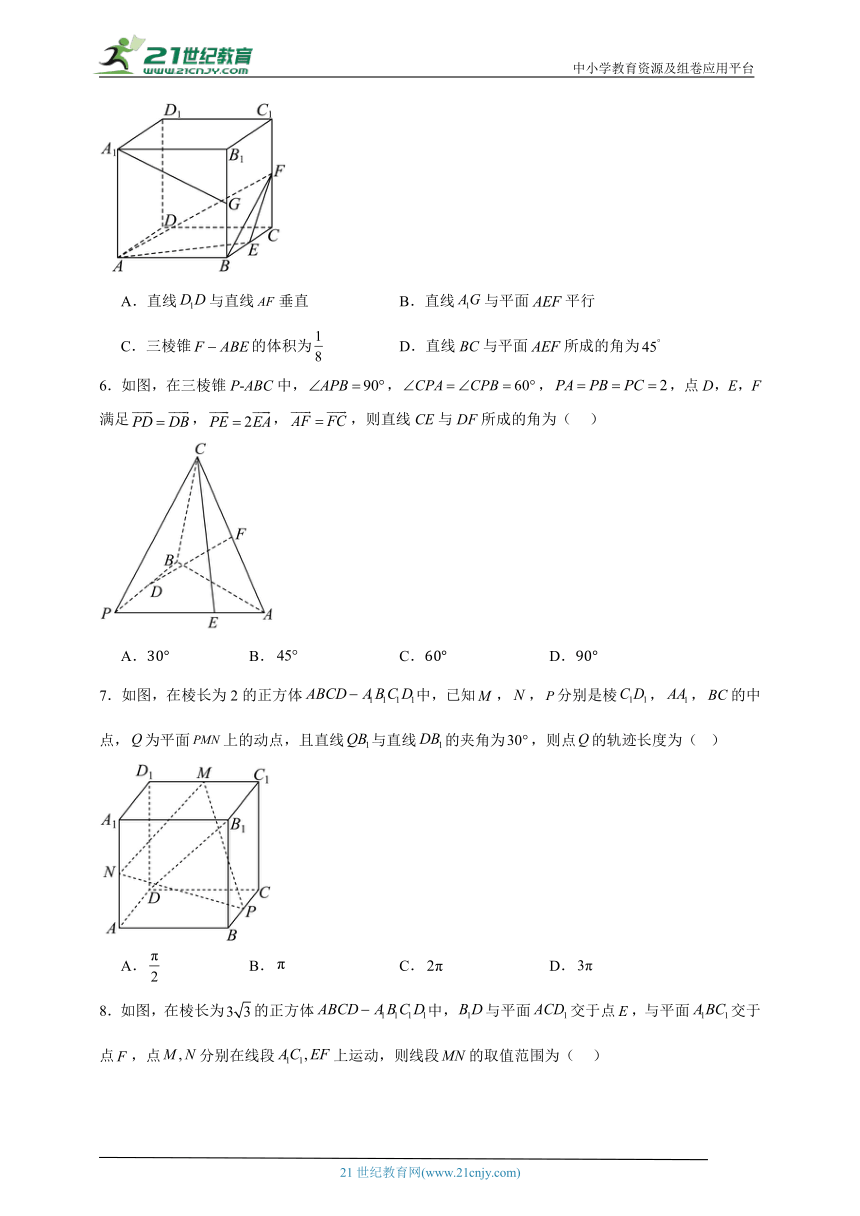
中小学教育资源及组卷应用平台 2024-2025学年高三数学上学期一轮复习专题：空间向量与立体几何 一、单选题 1．已知空间向量，若共面，则实数 （ ） a．1 b．2 c．3 d．4 2．如图，在平行六面体中，为与的交点．若，则下列向量中与相等的是（ ） a． b． c． d． 3．边长为1的正方体中，，分别是，中点，是靠近的四等分点，在正方体内部或表面，，则的最大值是（ ） a．1 b． c． d． 4．已知e，f分别是棱长为2的正四面体的对棱的中点.过的平面与正四面体相截，得到一个截面多边形，则下列说法正确的是（ ） a．截面多边形不可能是平行四边形 b．截面多边形的周长是定值 c．截面多边形的周长的最小值是 d．截面多边形的面积的取值范围是 5．如图所示，正方体的棱长为1，点分别为的中点，则下列说法正确的是（ ） a．直线与直线垂直 b．直线与平面平行 c．三棱锥的体积为 d．直线bc与平面所成的角为 6．如图，在三棱锥p-abc中，，，，点d，e，f满足，，，则直线ce与df所成的角为（ ） a． b． c． d． 7．如图，在棱长为2的正方体中，已知，，分别是棱，，的中点，为平面上的动点，且直线与直线的夹角为，则点的轨迹长度为（ ） a． b． c． d． 8．如图，在棱长为的正方体中，与平面交于点，与平面交于点，点分别在线段上运动，则线段的取值范围为（ ） a． b． c． d． 二、多选题 9．如图，在底面为等边三角形的直三棱柱中，，，，分别为棱，的中点，则（ ） a．平面 b． c．异面直线与所成角的余弦值为 d．平面与平面的夹角的正切值为 10．如图，在平行六面体abcd﹣a1b1c1d1中，以顶点a为端点的三条棱长都是1，且它们彼此的夹角都是，m为a1c1与b1d1的交点．若，，，则下列说法正确的是（　　） a． b． c． d． 11．如图，一个棱长为6的透明的正方体容器（记为正方体）放置在水平面的上方，点恰在平面内，点到平面的距离为2，若容器中装有水，静止时水面与表面的交线与的夹角为0，记水面到平面的距离为，则（ ） a．平面平面 b．点到平面的距离为8 c．当时，水面的形状是四边形 d．当时，所装的水的体积为 三、填空题 12．在空间直角坐标系中，，若三点共线，则 . 13．已知正四面体的棱长为2，若球o与正四面体的每一条棱都相切，点p为球面上的动点，且点p在正四面体面acd的外部（含正四面体面acd表面）运动，则的取值范围为 ． 14．如图，长方体中，，点在线段上，且为线段的中点，若，则异面直线与所成角的余弦值为 ． 四、解答题 15．如图1，在矩形中，，，将沿矩形的对角线进行翻折，得到如图2所示的三棱锥，且. (1)求翻折后线段的长； (2)点满足，求与平面所成角的正弦值. 16．“阳马”是我国古代数学名著《九章算术》中《商功》章节研究的一种几何体，即其底面为矩形，一条侧棱垂直于底面的四棱锥．如图，四边形是边长为3的正方形，，． (1)证明：四棱锥是一个“阳马”； (2)已知点在线段上，且，若二面角的余弦值为，求的值． 17．如图，在斜四棱柱中，底面正方形的中心是，且为顶点在底面的投影. (1)证明：平面平面； (2)若该四棱柱的所有棱长均为1，求二面角的正弦值. 18．如图，已知四棱台的上、下底面分别是边长为2和4的正方形，平面平面abcd，，点p是棱的中点，点q在棱bc上． (1)若，证明：平面； (2)若二面角的正切值为5，求bq的长． 19．如图，已知四棱柱的底面为菱形，，，，，e是棱上的点． (1)求证：四棱柱为直棱柱； (2)若，求平面与平面夹角的余弦值． 参考答案： 1．a 【分析】根据空间向量共面定理可知存在一对有序实数，使，然后列方程组可求得答案. 【详解】因为不共线，共面， 所以存在一对有序实数，使， 所以， 所以，解得， 故选：a 2．b 【分析】利用空间向量基本定理表示出，得到答案． 【详解 ... ...